La Meccanica della Frattura è utilizzata per studiare la resistenza dei componenti meccanici in presenza di difetti o cricche. Infatti, l’approccio tradizionale alla verifica della resistenza, basato sul confronto degli sforzi presenti in un corpo per effetto dei carichi applicati con uno sforzo limite del materiale, a snervamento o a rottura a seconda dei casi, non è infatti applicabile quando vi siano difetti o cricche, caratterizzati da un raggio di raccordo teoricamente nullo, perché il calcolo dello sforzo restituisce un valore puntuale all’apice tendente all’infinito, indipendentemente dall’entità del carico applicato.
D’altro canto, difetti preesistenti, derivanti dal processo produttivo e dalle lavorazioni in esso coinvolte, o nucleati in conseguenza della ripetizione ciclica degli sforzi, come avviene nella fatica, sono in grado di determinare cedimenti catastrofici ed è quindi indispensabile disporre di una metodologia di calcolo affidabile per valutare la resistenza dei componenti meccanici in loro presenza.
La meccanica della frattura consente, a partire dallo sforzo applicato a distanza e dalle dimensioni e geometria della cricca, di calcolare un parametro denominato Fattore d’Intensità degli Sforzi, il cui confronto con una caratteristica del materiale, la Tenacità a Frattura, permette di giudicare le condizioni di resistenza del componente.
La meccanica della frattura è anche utilizzata per studiare l’aumento delle dimensioni di una cricca, cioè la sua propagazione, con la ripetizione dei cicli di sforzo e dà pertanto la possibilità di calcolare l’evoluzione nel tempo della resistenza del componente. Sulla possibilità di mettere o mantenere in esercizio un componente affetto da difetti fino a quando la resistenza residua sia sufficiente rispetto ai carichi applicati si basa l’approccio alla progettazione a fatica della Damage Tolerance.
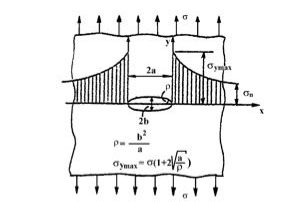
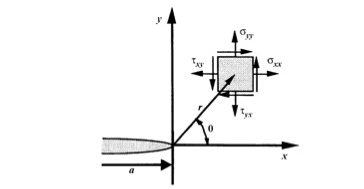
In figura 1 è mostrato l’andamento degli sforzi in prossimità di un intaglio ellittico: le equazioni riportate forniscono lo sforzo massimo locale e permettono pertanto il calcolo del coefficiente d’intaglio Kt.
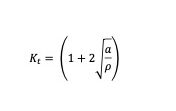
Lo sforzo massimo tende all’infinito al tendere a zero del raggio di raccordo, ma nella realtà, lo sforzo si ridistribuisce e si genera una zona plastica soggetta a valori finiti dello sforzo e, come anticipato, l’approccio basato sul coefficiente d’intaglio cade in difetto.
I modi della frattura
La meccanica della frattura considera tre diversi modi, denominati rispettivamente apertura in trazione (I), scorrimento nel piano o taglio (II) e scorrimento fuori piano o lacerazione (III). Nel seguito per semplicità si farà riferimento al primo modo, anche per la sua predominanza dal punto di vista pratico in gran parte dei casi.
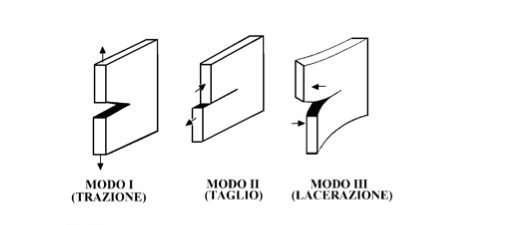
Prescindendo da altri termini, che divengono trascurabili con l’avvicinarsi all’apice, lo stato di sforzo in prossimità di una cricca può essere espresso, per il modo I, come segue:
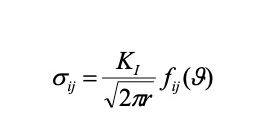
Gli effetti del carico applicato, della geometria e delle dimensioni della cricca sono contenuti nel parametro K (Fattore d’Intensità degli Sforzi o SIF – Stress Intensity Factor), che caratterizza il campo di sforzi in prossimità dell’apice, e che costituisce il termine di confronto per verificare la resistenza: il cedimento si verifica quando KI supera una proprietà del materiale denominata tenacità a frattura (KIC).
Dall’analisi dimensionale è possibile verificare che KI e KIC hanno dimensioni di uno sforzo per la radice quadrata di una lunghezza, tipicamente 𝑀𝑃𝑎√𝑚.
L’espressione generale di KI
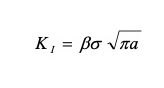
evidenzia la sua dipendenza dalla lunghezza della cricca (semilunghezza se la cricca è centrale e non di estremità), dallo sforzo applicato e da un fattore geometrico.
Componente sollecitato a fatica
Quando un componente è sottoposto ad una sollecitazione di fatica, cioè quando lo sforzo applicato varia da un valore minimo ad un valore massimo, anche il fattore d’intensità degli sforzi oscilla conseguentemente tra un minimo ed un massimo ciclicamente. È possibile stabilire una correlazione tra il tasso di avanzamento per ciclo della lunghezza della cricca e la variazione del fattore d’intensità degli sforzi (ΔK), come mostrato nel diagramma doppio logaritmico, che riporta in ascissa ΔK ed in ordinata da/dN.
Il diagramma è suddiviso in tre regioni (figura 4). La regione I mostra che, per valori di ΔK inferiori ad una soglia (ΔKTH, TH da Threshold) l’avanzamento per ciclo è nullo, cioè la cricca non propaga. In altri termini, fissata la lunghezza, è necessario superare una variazione minima di sforzo o, fissato lo sforzo, è necessario superare una lunghezza minima affinché si abbia propagazione. Superata la soglia, si ha un rapido aumento dell’avanzamento per ciclo, fino ad incontrare la regione II, nella quale si ha una crescita lineare (in diagramma bilogaritmico) dell’avanzamento per ciclo con ΔK. Nella regione III si assiste ad un rapido aumento di da/dN con ΔK, segno che con il valore massimo di K ci si sta avvicinando alla condizione di cedimento statico.

Nella regione II, il tratto lineare è descritto da un’equazione del tipo:
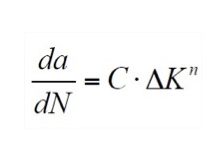
cioè dalla legge del Paris, la quale può essere utilizzata per determinare, mediante integrazione, l’andamento della lunghezza della cricca in funzione del numero di cicli. La legge del Paris è valida solamente nella zona II e trascura l’effetto del rapporto R di fatica (rapporto tra lo sforzo minimo e massimo applicato) che invece influenza l’avanzamento della cricca. Esistono leggi più complesse, in grado di tenere conto di R e della regione III, che qui non vengono considerate.
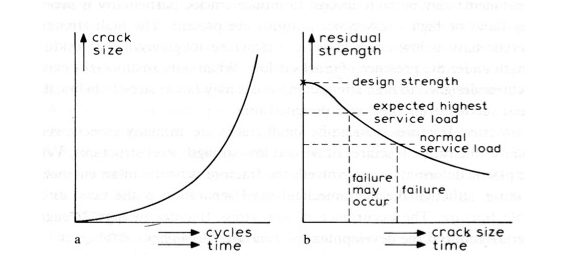
Nota la lunghezza della cricca in funzione del numero di cicli, e quindi del tempo, è possibile determinare la resistenza residua in funzione del tempo e pertanto stabilire quando si raggiunga una condizione di criticità che richieda la messa del componente fuori servizio (figura 5). Ciò costituisce l’essenza della progettazione con l’approccio della damage tolerance che, per essere completato, richiede l’applicazione di un piano di ispezioni periodiche mediante controlli non distruttivi.
(di Carlo Gorla)






